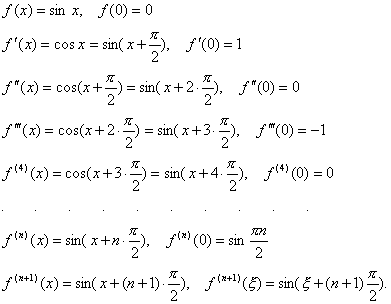Остаточный член в форме

Формула Тейлора с остаточным членом в форме Пеано, Лагранджа
Помочь проекту. Остаточный член в формуле Тейлора. Пусть функция f x бесконечно дифференцируема в точке. Тогда ей можно поставить в соответствие ряд 1. Если существует.










Конев В. Дифференцирование функций. Разделы курса Примеры Калькулятор. Пределы Неопределенные интегралы Определенные интегралы Несобственные интегралы.

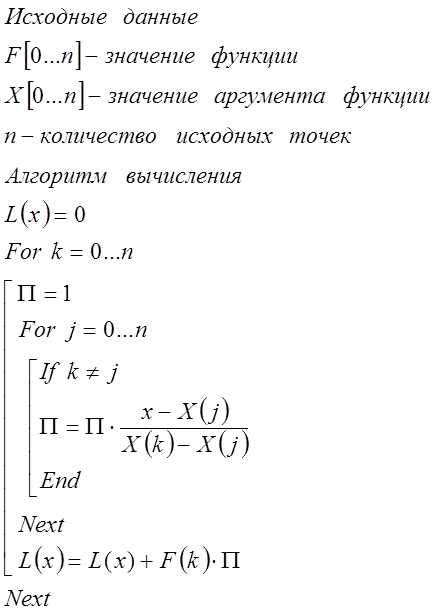





Выше мы установили формулу Тейлора с остаточным членом в общей форме. Здесь мы установим другие возможные представления для остаточного члена. Два из них могут быть получены в качестве частных случаев из общей формы. Прежде всего несколько преобразуем формулу для остаточного члена 6. Поскольку точка лежит между точками а и х, найдется такое число 0 из интервала что При этом Таким образом, формула 6.